Sens et écriture des nombres
Nombres naturels
L’utilisation du tableau de numération en 1re année est prématurée. L’accent est plutôt mis sur le groupement en utilisant du matériel aux groupements apparents et accessibles ou des dessins (matériel non structuré comme, par exemple, des jetons, des cubes emboîtables, des objets divers groupés par dix dans un sac, dont dix de ces sacs sont placés dans un autre contenant).
Ce n’est qu’à partir de la 2e année que l’accent est mis sur l’échange en utilisant du matériel aux groupements apparents et non accessibles (matériel structuré comme, par exemple, des blocs base 10, un tableau de numération). Aux 2e et 3e cycles, le tableau de numération est aussi utile pour travailler la valeur de position.
Références :
Programme de formation, p. 134
Progression des apprentissages, p. 5, no A-4 a-b-c
Le tableau de numération est un matériel qui sert à travailler autant les échanges que la valeur de position lors de la représentation des nombres.
Références :
Programme de formation, p. 134
Progression des apprentissages, p. 5, no A-4 b-c
Cette question s’inscrit dans le développement du sens du nombre et, plus particulièrement, l’apprentissage de la numération en base 10. La construction du concept de numération en base 10 se fait graduellement. Les six premiers énoncés de la section Sens et écriture des nombres (Progression des apprentissages, p. 5 et 6) et leurs savoirs essentiels correspondants (Programme de formation, p. 134) décrivent les premiers apprentissages de l’élève dans le développement du sens du nombre.
Diverses activités devront être proposées à l’élève. Il apprendra à compter, à dénombrer des collections réelles ou dessinées. L’élève dénombre une collection en comptant chacun des objets. Il sera amené à faire des groupements et à associer ces groupements à des nombres. Éventuellement, il sera amené à faire des échanges. De concert, il apprendra à lire et à écrire des nombres, et le vocabulaire associé sera introduit : unité, dizaine, centaine. Il sera incité à représenter des nombres naturels de différentes façons ou à associer un nombre à un ensemble d’objets ou à dessiner et à reconnaître des représentations équivalentes. Il serait intéressant de proposer à l’élève différents matériels de manipulation tels que jetons, objets, cubes emboîtables, blocs base 10, tableau de numération. Là où l’accent est mis sur la valeur de position, il y aura évolution du concret vers le symbolique.
Prenons un exemple. Tout d’abord, l’élève dénombrera 23 objets en les comptant un à un. Ensuite, il apprendra à faire différents groupements (dont les groupements de 10) et à dénombrer cette collection en se servant des groupements (ex. : il pourra compter en disant 10, 11, 12, … 22, 23 ou en disant 10, 20, 21, 22, 23). Il pourra écrire 23 et dire 23 ou 1 dizaine et 13 unités ou 2 dizaines et 3 unités. C’est en faisant réaliser des activités de ce genre que l’élève constate que le nombre 23 est composé de 2 dizaines et 3 unités, et il pourra représenter cette collection de différentes façons et reconnaître des représentations équivalentes.
La progression des apprentissages, telle qu’elle est présentée dans l’énoncé 4 de la page 5 du document, nous amène à penser qu’il serait probablement prématuré de poser des questions de ce type avant le 2e cycle.
Références :
Programme de formation, p. 134
Progression des apprentissages, p. 5 et 6, nos A-1, A-2, A-3, A-4, A-5 et A-6
Ex. : 84 123 = 8 x 104 + 4 x 103 + 1 x 10² + 2 x 10 + 3 x 1
Au primaire, l’élève ne va pas jusqu’à utiliser les exposants dans les décompositions. Il pourrait par exemple décomposer le nombre 84 123 comme suit :
84 123 = 80 000 + 4 000 + 100 + 20 + 3
84 123 = 80 000 + 4 100 + 20 + 3
84 123 = 8 X 10 000 + 4 X 1 000 + 1 X 100 + 2 X 10 + 3 X 1
84 123 = 84 X 1 000 + 12 X 10 + 3 X 1
84 123 = 8 dizaine de mille + 4 unités de mille + 1 centaine + 2 dizaines + 3 unités
84 123 = 84 unités de mille + 12 dizaines + 3 unités
84 123 = 4 X 21 000 + 3 X 40 + 3
84 123 = 2 X 42 000 + 130 – 7
Références :
Programme de formation, p. 134
Progression des apprentissages, p. 6, no A-5
En ce qui concerne l’utilisation des exposants, l’élève du 3e cycle calcule la puissance d’un nombre.
Ex. : Calcule 6³ 6 x 6 x 6 réponse 216
Ex. : Sur la rue des Félins, il y a cinq maisons. Dans chaque maison, il y a cinq chats. Chaque chat a attrapé cinq souris. Chaque souris avait mangé cinq arachides.
À l’aide d’exposants, écris le nombre total
- de chats 5 x 5 réponse 5²
- de souris 5 x 5 x 5 réponse 5³
- d’arachides 5 x 5 x 5 x 5 réponse 54
Références :
Programme de formation, p. 134
Progression des apprentissages, p. 12, no A-10
Fractions
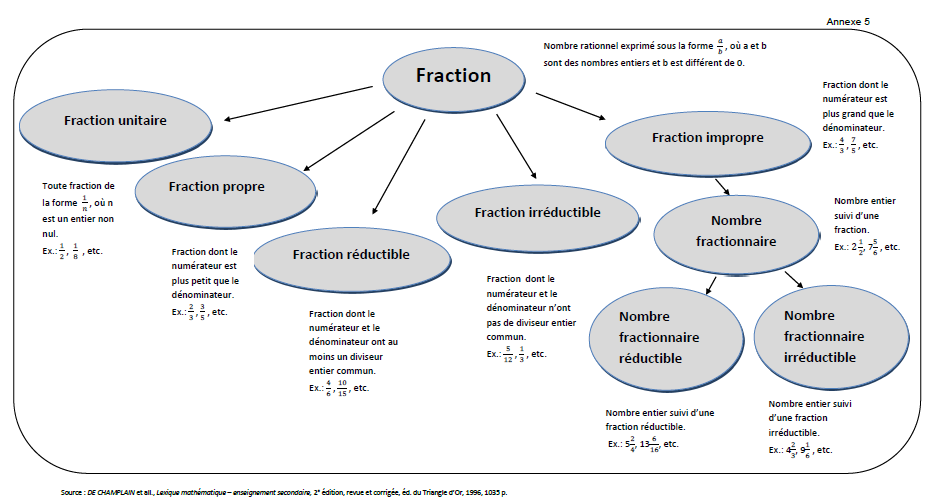
Un nombre fractionnaire est un nombre entier suivi d’une fraction (ex. : 2 , 7 ) alors que la notation fractionnaire est la représentation d’un nombre sous la forme d’un quotient de deux nombres ( ). Ainsi, 3 est un exemple de nombre fractionnaire exprimé en notation fractionnaire, et 3,5 est sa notation décimale. Les nombres fractionnaires sont abordés au primaire.
Références :
Programme de formation, p. 140 (Symboles)
Progression des apprentissages, p. 7, (Vocabulaire, 2e cycle)

Nombres décimaux
Le nombre 32 peut s’écrire avec des décimales. Ce n’est pas interdit, mais ce n’est pas toujours utile selon le contexte. C’est pertinent lorsqu’on veut comparer, ordonner et opérer et lorsque le contexte demande d’y recourir, comme, par exemple, dans un contexte d’argent. Décontextualisée, cette écriture pourrait soulever des questions : Pourquoi s’arrêter à 2 zéros à droite de la virgule et pourquoi ne pas en mettre 3?
Par convention, l’emploi de la virgule décimale indique que la position des unités est immédiatement à gauche de celle-ci. Par conséquent, quand il n’y a pas de partie décimale, elle n’est pas utile.
Références :
Programme de formation, p. 134
Progression des apprentissages, p. 7, nos C-3 et C-4
Voyons la limite de la grandeur des nombres à composer et à décomposer d’un élève de 2e cycle :
- la partie décimale du nombre se déploie jusqu’à l’ordre des centièmes;
- la partie entière du nombre est circonscrite à 100 000.
La section Sens et écriture d’un nombre – Nombres naturels (ci-haut) illustre plusieurs exemples de modèles de décomposition de la partie entière du nombre à décomposer.
Pour ce qui est de la partie décimale du nombre à décomposer, il est important que l’élève utilise une notation décimale. En voici quelques exemples :
- 6,31 = 6 + 0,3 + 0,01;
- 5,46 = 5 X 1 + 46 X 0,01;
- 1,5 = 15 X 0,1, car l’élève reconnaît des expressions équivalentes.
De plus, l’élève utilise en parallèle la notation fractionnaire dans la décomposition de nombres.
Exemple :
6,31 = 6 + 3⁄10 + 1⁄100 , car l’élève associe un nombre décimal à une fraction.
Dans une décomposition comme 12,3 = (1 x 10) + (2 x 1) + (3 x 1⁄10 ), l’utilisation de parenthèses n’est pas nécessaire, mais celles-ci peuvent être utiles pour visualiser la valeur de position des chiffres du nombre à décomposer. De même, l’utilisation du tableau de numération peut être utile pour faire voir la valeur de position des chiffres du nombre à notation décimale à décomposer.
Références :
Programme de formation, p. 134
Progression des apprentissages, p. 7 nos C-5, C-6 et B-9
Sens des opérations sur les nombres
Nombres naturels
Voici le document Les structures additives, qui résume les différents sens de l’addition et de la soustraction abordés au primaire. Les compositions de transformation s’y retrouvent.
Références :
Programme de formation, p. 135
Progression des apprentissages, p. 9, no A-2 b et c
Oui, avec les nombres à l’étude de son cycle. De plus, l’énoncé 5 de la page 12 de la Progression des apprentissages indique que l’élève du 1er cycle détermine les termes manquants dans une équation (Relation entre les opérations : Programme de formation, p. 135).
a + b = ?, a + ? = c, ? + b =c, a – b = ?, a – ? = c, ? – b =c
Ici, on remarque des équations de recherche de l’état initial, de transformation et de l’état final.
Références :
Programme de formation, p. 135
Progression des apprentissages, p. 9, no A-2 a
Progression des apprentissages, p. 12, no A-5
Dès le 1er cycle, lorsqu’on demande à un élève de déterminer un terme manquant dans une équation de type
a + b = ?, a + ? = c, ? + b =c, a – b = ?, a – ? = c, ? – b =c,
les relations entre les opérations sont présentes.
De même, avec les élèves du 2e et du 3e cycle, déterminer un terme manquant dans une équation de type
a x b = ?, a x ? = c, ? x b =c, a ÷ b = ?, a ÷ ? = c, ? ÷ b =c
fait développer le concept de relation entre les opérations.
Déterminer des équivalences numériques à l’aide de relations entre l’opération d’addition et la propriété des opérations commutativité de l’addition au 1er cycle où ( constitue une stratégie qui favorise la maîtrise des faits numériques de l’addition. Les équivalences numériques entre l’opération de la multiplication et la propriété des opérations commutativité de l’addition ( s’avère aussi une stratégie favorisant la maîtrise des faits numériques de la multiplication.
Le calcul mental met également à profit le sens des opérations par l’utilisation efficace des relations entre les opérations ainsi que leurs propriétés. Ces processus de calcul découlent souvent d’un transfert des modèles utilisés au cours de l’apprentissage du sens des opérations.
Ainsi, la propriété des opérations associativité est utile, entre autres, lorsque l’élève utilise une stratégie de calcul mental telle que Additionner en complétant le premier terme à la dizaine comme dans l’exemple suivant :
47 + 14 = 47 + (3 + 11)
= (47 + 3) + 11
= 50 + 11
= 61
De même, la propriété des opérations distributivité est utile, entre autres, à l’intérieur d’une stratégie de calcul mental telle que Multiplier en décomposant le multiplicateur (2e facteur) :
23 x 12 = 23 x (10 + 2)
= (23 x 10) + (23 x 2)
= 230 + 46
= 276
Références :
Programme de formation, p. 135
Progression des apprentissages, p. 9, nos A-5 a, b, c, p. 10, nos B-3 a et b, p. 11, no A-2 b, p. 12 no A-6 b et p. 12 nos A-5 et A-8
Nombres décimaux
Lorsqu’on multiplie un nombre décimal par un nombre naturel, l’addition répétée est un sens de la multiplication qu’on peut choisir.
3,25 X 3 = ?
3,25 + 3,25 + 3,25 = ? Addition répétée 3 fois du « 3,25 »
9,75
Mais lorsqu’on multiplie un nombre décimal par un nombre décimal, le sens d’addition répétée perd son sens.
3,2 X 3,5 = ?
On peut additionner 3,5 trois fois, mais que faire du 0,2 qui reste?
Référence : Progression des apprentissages, p. 10, no B-2
Opérations sur les nombres
Nombres naturels
Le document Progression des apprentissages constitue un complément au Programme de formation. Il apporte des précisions sur les savoirs essentiels du Programme de formation, en les détaillant le plus possible dans l’idée d’une progression des apprentissages.
Le développement du répertoire mémorisé de la multiplication et de la division se fait au 2e cycle, d’abord avec la construction des faits numériques qui est prescrit au Programme à l’aide de matériel, de dessin, d’une grille ou d’une table, puis avec le développement de stratégies qui favorisent la maîtrise des faits numériques et l’établissement de liens aux propriétés de la multiplication (commutativité de la multiplication, 1 élément neutre et 0 absorbant). Enfin avec tout le travail de construction et de développement, arrive la maîtrise de l’ensemble des faits numériques. Pour s’assurer d’une maîtrise du répertoire mémorisé à long terme, l’élève a besoin d’une année supplémentaire.
Le raisonnement est le même pour le répertoire mémorisé de l’addition et de la soustraction.
Références :
Programme de formation, p. 135
Progression des apprentissages, p. 12, no A-6 a-b-c, et p. 11, no A-2 a-b-c
Pour l’addition, l’élève construit les faits numériques de 0 + 0 = 0 jusqu’à 10 + 10 =20.
Les soustractions correspondantes sont de 20 – 10 = 10 à 0 – 0 = 0.
(ex. : la table du nombre 8 :
0 + 8 = 8 8 + 0 = 8 8 – 0 = 8 8 – 8 = 0
1 + 8 = 9 8 + 1 = 9 9 – 1 = 8 9 – 8 = 1
2 + 8 = 10 8 + 2 = 10 10 – 2 = 8 10 – 8 = 2
3 + 8 = 11 8 + 3 = 11 11 – 3 = 8 11 – 8 = 3
4 + 8 = 12 8 + 4 = 12 12 – 4 = 8 12 – 8 = 4 etc.)
Pour la multiplication, l’élève construit les faits numériques de 0 X 0 = 0 jusqu’à 10 X 10 = 100.
Les divisions correspondantes sont de 100 ÷ 10 = 10 jusqu’à …
(ex. : la table du nombre 8 :
0 x 8 = 0 8 x 0 = 0 0 ÷ 8 = 0 8 ÷ 0 = Erreur
1 x 8 = 8 8 x 1 = 8 8 ÷ 8 = 1 8 ÷ 1 = 8
2 x 8 =16 8 x 2 = 16 16 ÷ 8 = 2 16 ÷ 2 = 8
3 x 8 = 24 8 x 3 = 24 24 ÷ 8 = 3 24 ÷ 3 = 8
4 x 8 = 32 8 x 4 = 32 32 ÷ 8 = 4 32 ÷ 4 = 8 etc.)
Références :
Programme de formation, p. 135
Progression des apprentissages, p. 11, no A-2 et p. 12, no A-6
Au 1er cycle, les élèves développent des processus de calcul écrit à l’aide de processus personnels, en utilisant du matériel ou des dessins. Ils déterminent la somme ou la différence de 2 nombres naturels inférieurs à 1000.
Références :
Programme de formation, p. 135
Progression des apprentissages, p. 11, no A-4 a
Il est important de se rappeler que les processus personnels ne s’enseignent pas : ils proviennent des élèves, ce sont eux qui les développent. En ce qui concerne le développement des processus personnels, le rôle de l’enseignant est de s’assurer de fournir aux élèves des problèmes mathématiques qui comportent différents sens de l’addition et de la soustraction (ajout, retrait, réunion, comparaison et complément), d’aider l’élève à organiser ses traces, de faire dire ce que l’élève fait et, par le fait-même, de l’aider à établir des liens entre le processus personnel développé et le concept mathématique sous-jacent et d’animer des échanges portant sur les processus utilisés par les élèves de la classe.
Au primaire, à l’apprentissage des opérations, l’élève développe des processus personnels pour donner du sens aux opérations, c’est une étape très importante de la construction du sens des opérations. Par exemple, pour la division, l’élève peut d’abord procéder par soustractions répétées, partage, etc., pour déterminer le quotient. Par la suite, au 3e cycle, il utilisera un processus conventionnel pour exécuter l’opération. (On entend ici l’algorithme de division « traditionnel » de calcul écrit). Au primaire, on amène l’élève à faire le transfert des processus personnels vers les processus traditionnels à l’aide de matériel concret ou de schémas. Puis au secondaire, l’élève effectue ce qu’il a développé au primaire.
Références :
Programme de formation, p. 142
Progression des apprentissages, p. 9, no A-3 b et p. 12, no A-7c
Un processus de calcul conventionnel est une technique opératoire reconnue avec une suite de règles à appliquer à un nombre de données, dans un ordre déterminé, pour arriver avec certitude à un résultat, et ce, indépendamment des données.
Le Programme de formation et la Progression des apprentissages indiquent « qu’à tous les cycles, l’utilisation de la calculatrice doit se faire à bon escient comme outil de calcul, outil de vérification ou outil d’apprentissage ».
Elle est utilisée :
- pour l’exploration des nombres naturels, des nombres décimaux, des fractions et des nombres entiers;
- pour l’exploration des opérations avec les nombres naturels, les nombres décimaux et les fractions;
- pour exécuter les opérations avec les nombres qui dépassent les limites du programme;
- pour faire la preuve des opérations;
- pour la résolution de situations-problèmes comportant plusieurs étapes, où l’accent est mis sur le raisonnement, la recherche et la mise en place de stratégies mobilisant des connaissances plutôt que sur le processus de calcul.
La calculatrice n’est pas un processus de calcul conventionnel.
Il est aussi intéressant d’utiliser d’autres outils technologiques que la calculatrice.
Références :
Programme de formation, p. 142
Progression des apprentissages, p. 11, Introduction du tableau et p. 12, no A-15 a-b-c
Une régularité correspond à un phénomène qui se produit selon une loi ou une règle de formation qui s’applique à un ensemble. Il y a une régularité lorsqu’on peut énoncer des propriétés d’un ensemble ou établir une formule mathématique.
Une suite de nombres établie d’après une règle de formation qui permet de retrouver chaque terme est un exemple de régularité.
Exemples :
2, 5, 8, 11, 14, … la règle est n + 3 où n représente le terme précédent;
1, 2, 4, 8, 16, … chaque terme de la suite est le double du terme précédent;
3, 2, 5, 4, 7, 6, 9, … on observe ici la régularité « -1 + 3 »
1, 2, 5, 10, 17, … on observe la régularité « + 1 + 3 + 5 + 7 … »
Les ensembles suivants en sont d’autres exemples.
OO OOOO OOOOOO OOOOOOOO Il est composé successivement de 2, 4, 6 et 8 disques.
Δ ♥ ♦ Δ ♥ ♦ Il est composé successivement d’un triangle, d’un coeur et d’un losange.
Les frises et les dallages sont aussi des exemples de régularités.
Pour développer le sens des nombres et des opérations dans ce contexte, l’élève observe différentes régularités. Il reconnaît des régularités, en construit, trouve des termes manquants à l’intérieur des suites, les prolonge, les décrit à l’aide de mots qu’il connaît et du langage mathématique propre à son cycle. Pour y arriver, il détermine les opérations en cause.
L’expression « famille » a plusieurs acceptions et correspond, entre autres, à une propriété commune à un ensemble donné. Elle peut être associée à plusieurs éléments. Dans certaines références, on peut lire, par exemple, « famille des fractions équivalentes à 2⁄3 : 4⁄6, 6⁄9,8⁄12».
« Famille d’opérations », dans le contexte de régularité, peut être vue notamment comme la ou les opérations communes d’une suite de nombres. Par exemple, les tables d’addition et de multiplication contiennent de nombreuses régularités. On peut y dégager plusieurs familles d’opérations, car elles ont des propriétés communes liées à une ou à des opérations.
Ces exemples en sont d’autres où l’on peut reconnaître une régularité et dégager une propriété commune :
Les multiples de 5 : 5, 10, 15, 20, …
« Un de plus » à partir d’un nombre donné : 4, 5, 6, 7, …
« -3 » ou retrancher 3 : 14, 11, 8, 5,…
Ce n’est pas le terme « familles » qui est important ici, mais la reconnaissance de la régularité.
Références :
Programme de formation, p. 136
Progression des apprentissages, p. 12, no 13
Non, car une table de valeurs est un registre qui permet de visualiser un lien de dépendance entre deux éléments, alors qu’un tableau est utilisé pour organiser des données où il n’y a pas nécessairement de liens de dépendance entre celles-ci.
Références :
Programme de formation, p. 138
Progression des apprentissages, p. 20, nos 2, 3 a, 3 b, 3 c, 4 a, 4 b et vocabulaire correspondant
Puisque l’élève du 3e cycle peut calculer la puissance d’un nombre, les exposants peuvent aussi se retrouver dans les chaînes d’opérations à effectuer.
Cependant, appliquer l’exposant sur une parenthèse revient à faire davantage que simplement calculer la puissance d’un nombre, mais il est possible de retrouver l’exposant sur un nombre à l’intérieur même de la parenthèse, comme par exemple : (2 + 3²).
Références :
Programme de formation, p. 134-135
Progression des apprentissages, p. 12, nos A-10 et A-12
Fractions
Les nombres fractionnaires font partie des fractions et ils sont abordés au primaire.
Ici, le nombre fractionnaire 2 2⁄6 a un dénominateur qui est le multiple du dénominateur de la fraction 1⁄3 . L’élève du 3e cycle du primaire est en mesure de faire cette addition.
Références :
Programme de formation, p. 136
Progression des apprentissages, p. 12, no B-1, p. 12, no B-2 et p. 12, no B-3
La recherche du PPCM est utile pour additionner ou soustraire des fractions dont les dénominateurs ne sont pas les multiples de l’un ou de l’autre. Au primaire, les opérations d’addition et de soustraction de fractions se font à l’aide de matériel concret ou de schémas. L’élève du 3e cycle n’additionne et ne soustrait que des fractions dont le dénominateur de l’une est le multiple de l’autre. C’est plutôt en passant par la recherche de fractions équivalentes, à l’aide de matériel concret ou de schémas, que l’élève donnera du sens à la procédure d’addition et de soustraction de fractions.
Bien que le moyen le plus rapide pour arriver à la fraction irréductible est de diviser le numérateur et le dénominateur par leur PGCD, l’élève du 3e cycle du primaire, à l’aide de matériel concret ou de schémas, réduit une fraction à sa plus simple expression en passant, entre autres, par les fractions équivalentes, où le numérateur et le dénominateur n’ont plus de diviseur commun autre que 1 comme dans l’exemple suivant.
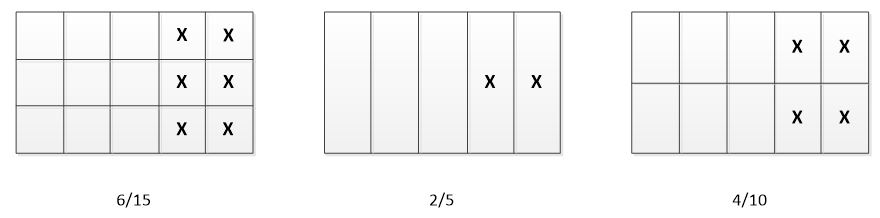
Il existe une fraction de chaque famille de fractions équivalentes (2⁄5dans l’exemple ci-dessus) dont les termes n’ont plus de diviseur commun différent de 1. Cette fraction s’appelle irréductible.1
Les termes PPCM et PGCD sont absents du Programme de formation et de la Progression des apprentissages au primaire. Au secondaire, ces propriétés sont exploitées dans différents contextes, dans la recherche ou la production d’expressions équivalentes et dans les opérations sur des nombres.
Références :
Programme de formation, p. 136
Progression des apprentissages, p. 12, nos B-2, B-3 et vocabulaire correspondant
1 ROEGIERS, Xavier, Les mathématiques à l’école primaire, Tome 1, p. 163.
Nombres décimaux
Oui, lorsque, à l’aide de processus personnels (utilisation de matériel ou de dessins), il est question de déterminer le quotient d’un nombre naturel à 3 chiffres par un nombre naturel à 1 chiffre, les élèves du 2e cycle expriment le reste de la division sous la forme d’une fraction.
Mais, lorsque, à l’aide de processus conventionnels, il est question de déterminer le quotient d’un nombre naturel à 4 chiffres par un nombre naturel à 2 chiffres, les élèves du 3e cycle expriment la réponse sous forme d’un nombre en écriture décimale sans dépasser la position des centièmes.
Références :
Programme de formation, p. 135
Progression des apprentissages, p. 12, no A-7 a et c
Pour ce qui est de la division d’un nombre décimal par un nombre naturel inférieur à 11, les élèves du 3e cycle expriment la réponse sous forme d’un nombre en notation décimale sans dépasser la position des centièmes comme ils le font avec la division des nombres naturels. Lorsque l’élève effectue la division, il « s’arrête » lorsque le reste de la division atteint la position des centièmes.
Références :
Programme de formation, p. 135 et 136
Progression des apprentissages, p. 13 no C-3 c et p. 12, no A-7 c
Les élèves du 3e cycle peuvent arrondir à l’ordre des centièmes, en poursuivant la division jusqu’à l’ordre des millièmes, puis arrondir aux centièmes.
Le terme « périodique » ne fait pas partie du vocabulaire des élèves du primaire. Les élèves constatent tout simplement que le chiffre se répète.
Références :
Programme de formation, p.135 et 136
Progression des apprentissages, p. 13, no C-3 c, p. 12, no A-7 c et p. 7, no C-9
Utilisation des nombres
Au primaire, c’est le sens du concept de pourcentage qui doit être développé prioritairement. La recherche du pourcentage passe par la recherche de fractions équivalentes.
Au secondaire, le calcul du « tant pour cent » proprement dit et la recherche du « cent pour cent » pourront se faire par le raisonnement proportionnel.
Références :
Programme de formation, p. 134
Progression des apprentissages :
- 7, no B-9 : Associer un nombre décimal ou un pourcentage à une fraction
- 12, no B-1 : Construire un ensemble de fractions équivalentes
- 13, no D-3 : Exprimer par un pourcentage un nombre exprimé en notation fractionnaire et vice versa
C’est par le passage à la notation fractionnaire ou à la notation décimale et en faisant le lien avec les apprentissages réalisées au regard des fractions et des nombres décimaux que l’élève du primaire est initié et est en mesure de calculer 10 % de 40.
10 % = 10⁄100 = 1⁄10 donc 10 % de 40 c’est 1⁄10 de 40.