Souvent, les élèves du 1er cycle font des activités de repérage sur un axe et dans un plan avant d’être initiés au plan cartésien. L’introduction au plan cartésien se fait de manière informelle et ludique (ex. : les jeux de bataille navale et d’échecs). Ces activités se font dans le premier quadrant du plan cartésien avec des nombres naturels à l’étude. La description des déplacements sur les planches de jeux ou des échiquiers initie les élèves au système de repérage cartésien et à l’écriture des coordonnées.
Références :
Programme de formation, p. 136
Progression des apprentissages, p. 14, nos A-4a et A-3, p. 6, no A-10
Progression des apprentissages, p. 14, A, Symboles
À partir du 2e cycle, l’élève identifie et construit des droites parallèles et des droites perpendiculaires. Il utilise diverses stratégies de construction en utilisant, par exemple, des règles, des équerres, du papier quadrillé ou pointé. De cette façon, il trace des angles droits (avec les droites perpendiculaires) et des droites parallèles, qui lui permettront ensuite de construire le carré et le rectangle, par exemple. Dans ce contexte, l’utilisation du rapporteur d’angles pour tracer un angle droit n’est pas nécessaire. Après avoir fait développer ces stratégies de construction en classe, il n’est pas impossible d’évaluer l’élève sur sa capacité à tracer des droites parallèles et des droites perpendiculaires en lui demandant de construire une figure comme un carré, mais il faut considérer que cette tâche est plus compliquée. On peut vérifier l’acquisition de ces concepts dans d’autres contextes.
Pour ce qui est de l’énoncé Comparer et construire des figures composées de lignes courbes fermées ou de lignes brisées fermées, on remarque qu’il est développé au 1er cycle. Il s’agit ici du développement de la représentation des figures où la construction des figures sera faite sans grande précision, à main levée ou à l’aide de papier quadrillé.
Références :
Programme de formation, p. 136-137
Progression des apprentissages, p. 15, nos C-1 et C-5
Au primaire, l’élève du 1er cycle compare, construit et identifie la boule, le cône, le cube, le cylindre, le prisme et la pyramide. Il identifie et représente les faces d’un prisme ou d’une pyramide. L’élève du 2e cycle décrit des prismes et des pyramides à l’aide de faces, de sommets et d’arêtes. L’élève du primaire n’a pas à décrire les corps ronds à l’aide des attributs faces, sommets et arêtes : il ne le fait qu’avec les prismes et les pyramides.
Références :
Programme de formation, p. 136
Progression des apprentissages, p. 14, nos B-2 et B-3, p. 15, nos B- 4 et B-5
Apex est le nom donné à certains sommets remarquables (cône, pyramide, sommet opposé à la base d’un triangle).
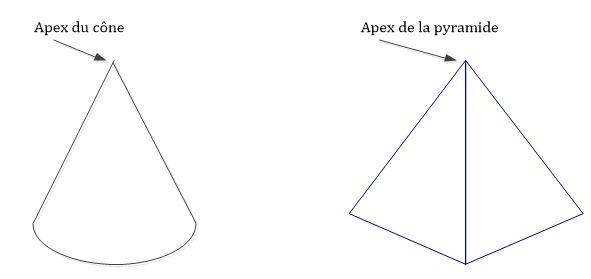
Par contre, au sujet des solides au 1er cycle du primaire, la Progression des apprentissages précise qu’on les compare, les construit et les identifie. On observe la base, les faces et les surfaces planes ou courbes d’un solide. On ne les décrit pas à l’aide de leurs composantes apex, directrice et génératrice.
Ce n’est qu’au 2e cycle, avec les prismes et les pyramides qu’on décrit ces solides à l’aide de leurs faces, de leurs sommets et de leurs arêtes.
Références :
Programme de formation, p. 136
Progression des apprentissages, p. 14, nos B-2, B-3 et vocabulaire correspondant, p. 15, no B-5